Del 2 i ”Tänkarskola för beslutsfattare” bygger vidare på ”#1 Den mänskliga kausaldriften” och handlar om begreppen korrelation och kausalitet, och skillnaden mellan dem. Som beslutsfattare är det absolut nödvändigt att känna till och förstå dessa begrepp.
Korrelation och kausalitet förväxlas ofta, men korrelation inom statistiken är ett uttryck för styrkan och riktningen av ett linjärt samband mellan två (eller flera) variabler. En variabel kan vara vad som helst: längd, vikt, lön, temperatur eller priset på en bil.
Korrelationen kan räknas ut (den s.k. korrelationskoefficienten, r), och blir då ett tal mellan +1 (100 % positiv korrelation) och -1 (100 % negativ korrelation). Om talet blir 0 finns ingen korrelation, vilket innebär att det inte finns något linjärt samband. (Men det kan ändå finnas ett icke-linjärt samband.)
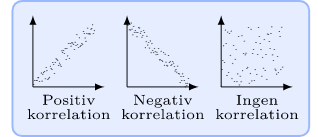
Själva korrelationen mellan två fenomen A och B, hur stark den än är, säger däremot ingenting om hur ett eventuellt orsakssamband (kausalt samband) mellan variablerna ser ut.
Det kan ju finnas någon typ av kausalt samband bakom en korrelation, men för att fastställa det behövs ofta någon form av djupare analys (se klippet om ”kausala nätverk” längre ner).
Förenklat kan ett kausalt samband t.ex. vara något av följande:
A => B ————– A orsakar B
A <= B ————– B orsakar A
A => C <= B ——- A och B orsakar båda C
A <= C => B ——- C orsakar både A och B, men A och B orsakar inte varandra direkt.
Det allra sista sambandet kan man kalla ett skensamband mellan A och B, något som är
mycket vanligt i det verkliga livet. Problemet är ofta att komma på vad C är.
Det finns också samband där A och B påverkar varandra, utan att direkt orsaka varandra (ömsesidigt samband).
Skrivet så här kan det tyckas stelt och matematiskt, men varenda dag bedömer våra hjärnor mängder av sanna och falska orsakssamband. Många av dem är tydliga och enkla, men lika många är dolda och komplexa – eller finns helt enkelt inte.
Här är ett exempel från en diskussion på LinkedIn:
- Påstående: Att gå upp 05.00 (A) skapar framgång (B). (A => B)
- Men det kan ju lika väl vara tvärtom, dvs:
Framgång (B) driver en individ att gå upp 05.00 (A). (A <= B) - Eller: en tredje faktor (C) ligger bakom både att en individ går upp tidigt (A) och framgång (B), dvs A <= C => B. Här finns det alltså inget direkt samband mellan A och B, utan ett skensamband med C som gemensam orsak.
Följande pedagogiska film vidgar resonemangen kring kausalitet:
(För den som vill fördjupa sig ytterligare i systemteori har Youtube-kanalen ”Systems Innovation” många fler videor – både grundläggande och mer avancerade.)
Mängder av intuitivt kausala samband som vi människor uppfattar i vardagen och i arbetslivet är korrekta, men samtidigt är väldigt många också…helt fel.
Detta är mycket viktigt för beslutsfattare i företag och andra organisationer att förstå. Vad ger olika åtgärder i företaget för effekter? Är det verkligen A => B eller är det i själva verket A <= B? Och är det ett äkta kausalt samband eller ett skensamband (A<= C =>B)? Och vad är i så fall C…?
Här är två pedagogiska videor till. Den första tar upp lite allmänt om korrelation vs. kausalitet (orsakar verkligen glass eldsvådor?). Den andra gör en djupare analys av korrelation och möjlig kausalitet utifrån studien ”Eating breakfast may beat teen obesity” – ett utmärkt exempel på hur viktigt det är att tänka till lite extra när man läser publicerade studier.
Som lite överkurs tar jag med följande korta Youtube-klipp också, från Minutephysics. Det tar upp begreppet ”kausala nätverk”, som ibland kan användas för att analysera sig fram till kausalitet utifrån korrelation.
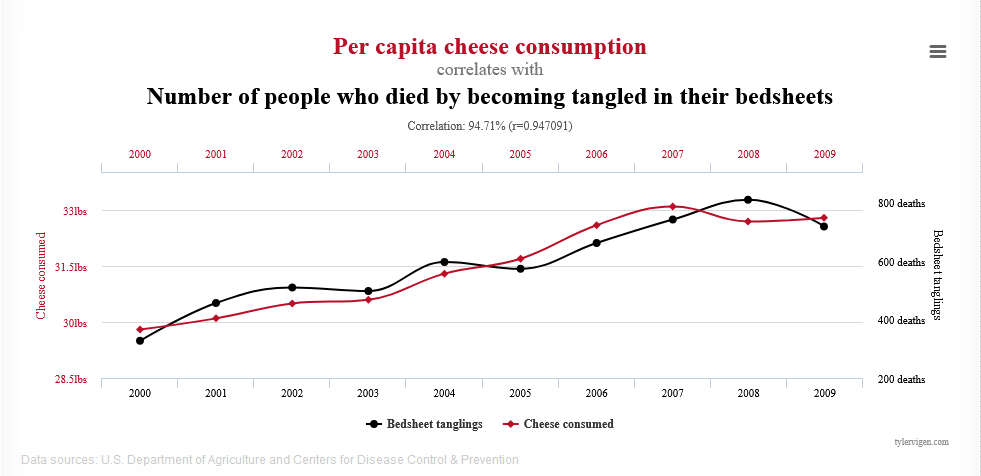
Hur galet det kan bli om man letar upp korrelationer mellan vitt skilda fenomen kan du se på den kända hemsidan Spurios Correlations.
I det här exemplet visas korrelationen (USA, år 2000-2009) mellan ostkonsumtion per capita och antalet personer som dött till följd av att ha snärjt in sig i sina lakan. Korrelationen är här 94,71%. Kausalt samband…?
Tack för uppmärksamheten!

